What is Chaos Theory? – Science Made Easy

Perhaps you may have heard the term “butterfly effect”. It is one of the most famous and maybe intriguing examples to explain what chaos theory is and what it proposes to our lives. A flap of a butterfly’s wing in let’s say in Dublin can create a tornado in Australia. For a more general description, small things can create huge impacts on complex systems.
In our example, the butterfly of course solely does not create a tornado, but such small events and starting conditions can act as catalysts and lead to alterations in the system, creating domino effects. If the butterfly had not flapped its wings, the tornado might have never happened. The tricky part is without our little butterfly’s flapping, there would also be conditions that lead to a tornado. The flap of the wings is a part of the initial conditions of an interconnected complex web; one set of conditions leads to a tornado while the other set of conditions doesn’t.
This is what makes predicting things hard for us. Because we can’t know our initial conditions in full accuracy. Let’s consider weather prediction. To make a prediction, meteorologists take a lot of observational data from land, sea, and air. Then this data is evaluated with complex mathematical models in supercomputers to create a prediction. The computers need to take into account data with multiple variables and factors. Since long term predictions require vast amounts of data and contain too many unpredictable factors, we can’t successfully make them. However, some ways facilitate our projections’ reliability. The story starts with a meteorologist from MIT. He discovered the butterfly effect and later on created the chaos theory.
[youtube https://www.youtube.com/watch?v=r_5shyQGIeA&w=560&h=315]
Story of a Meteorologist
Edward Lorenz was a meteorology professor at MIT in the 1960s. In the conventional wisdom at the time, they were convinced that if we could give our computers the right measurable data for weather such as wind, temperature, and velocity, we could predict the weather. So with that idea in mind, Mr Lorenz constructed a simple set of equations and then programmed them on the computer. At the first attempts, the program was able to predict the weather only a few minutes ahead. Each time, Lorenz fed the program with the predicted weather. Then minutes added up to days and weeks.
One day, he decided to rerun the program, but he did not want to do it from scratch, so he used the predictions from halfway through the first run as a starting point. This meant that instead of using 0.506127, he used 0.506. He, like other scientists in the day, thought this would not result in a vast difference, but it did. This is how he discovered the so-called butterfly effect. This was the seeds of chaos theory as well.

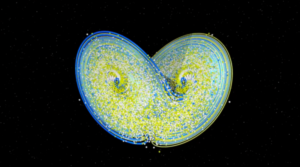
It is astonishing to think that two data starting so similarly but with a slight difference can end up with such different results. A difference so big that they would be in different regions in the cloud of information. On the contrary, if we take a large number of different initial conditions, then after a while they all land on the same object.

Hence, Lorenz’s equations created opposing purposes: repulsion routes within the data set and attraction beyond it. We call these complex systems “strange attractor” and the specific dynamics the “Lorenz attractor”. Many attractors were found after the discovery of Lorenz.
What is Chaos Theory?
The elegance is when you look closely at these strange attractors you can see fractals, repeating patterns. This means that even though we cannot fully comprehend a complex system, we can find ongoing similarities. Think about the chaotic systems in your everyday lives. For instance, stock markets, climate, road traffic, and even heart irregularities. They all contain repetitions.
Chaos theory is the study of these patterns by analysing chaotic mathematical models. Therefore, this is what helps us implement more successful predictions.
For me, chaos theory is not only a branch of mathematics. It is the science of surprises and it teaches us to expect the unexpected.
Poetically, even when you think in some situations there is nothing for you to rely on, you can always find a familiar sense, and I think this is beautiful.
